
5. Alkalmazhatóság vizsgálat
GPS méréseim célja - mint említettem - tájfutó térképek készítéséhez ismeretlen terepi pontokról GIS adatgyűjtés. Egyfelől az alkalmazás újdonságából, összefüggésben a rendelkezésre álló műszerekből, az alkalmazható mérési módszerek jelen hazai lehetőségeiből, korlátaiból fakadóan, másfelől a magyar tájfutó terepek jelentős része technikánk befogadását tekintve közel sem ideális, alapvető fontosságú az alkalmazhatóság fizikai lehetőségeinek, körülményeinek, esetleges korlátainak tisztázása. Különösen így van ez választott területemen a Bükk-hegységben, ahol tudomásom szerint ilyen jellegű kísérlet még nem volt, s tágabb környezetében sem történt.
Hogyan értékeljük, ítéljük meg és kalibráljuk az ismeretlen területen mérési eredményeinket? Az alkalmazhatóság és annak körülményei jól tisztázhatók a területre eső - ha van ilyen - ismert koordinátájú pontokra (referencia pontok) támaszkodva, ott ellenőrző méréseket végezve, majd a tapasztalatok kiértékelése útján.
5.1. Referencia pontok
Választott, bemutatandó területem a Bükk-hegységben, Bükkszentkereszt község környékén található. A területre esően két háromszögelési pont koordinátáit sikerült megszereznem. Az MH TÉHI szíves közlése szerint konkrét adataik a következők:
|
Referencia pont EOV száma: |
87-4213 |
|
|
|
EOV koordináta |
Y=767916,53 |
X=299710,50 |
h=596,07 |
|
Gauss-Krüger koordináta |
Y=4472415,21 |
X=5321986,62 |
|
|
Referencia pont EOV száma: |
88-3104 |
|
|
|
EOV koordináta |
Y=768608,52 |
X=302389,32 |
h=681,20 |
|
Gauss-Krüger koordináta |
Y=4473174,02 |
X=5324647,16 |
|
Az átszámított Gauss-Krüger koordináták hibája nem haladja meg a 15 cm-t.
Magyarország területén a meglévő EOV alappont hálózat mellett 1995-től kezdődően kiépült az 1153 pontból álló OGPSH (Országos GPS Hálózat). Sok esetben az OGPSH pontjai hagyományos alappontok, hiszen ha jó kilátással rendelkeznek az égbolt felé, és jól megközelíthetőek, már megfelelnek GPS felhasználásra. A GPS alappont hálózat tulajdonosa a FÖMI, a pontok koordinátáinak pontossága jobb mint 2 cm-es. [11]
Területem közvetlen közelében is található egy GPS alappont, melyek adatait munkám során szintén figyelembe vehettem: (A Kerti's Kft szíves közlése)
|
Referencia pont EOV száma: |
87-2419 |
|
|
|
EOV koordináta |
Y=767615,38 |
X=304429,33 |
HGPS=665,55 |
|
WGS-84 koordináta |
j =48° 04'21,84" |
l =20° 37'32,64" |
h=707,79 |
5.2. A mintavétel, a mérési terv ismertetése
Referencia méréseim helyét, GPS-eszközeit, az alkalmazható mérési módszereket, az észlelések feldolgozásának, értékelésének technikáját a rendelkezésre álló lehetőségek határozták meg:
5.3. A mérési minták értékelése
A fenti terv szerint elvégzett méréseim eredményeit a GPS műszerekből
letöltve, Excel-be konvertálva táblázatok tartalmazzák.5.3.1 A műszerek alapbeállítása, s összefüggésben: a feldolgozásból kizárt tételek és azok okai
A mérés és működés alapvető hibáit a berendezések önmaguk kijelzik. A jó mérési eredmények elérésére, másfelől a csökkent megbízhatóságú észlelések kiszűrése érdekében elvárásainkat ugyanakkor a műszerek megfelelő alapbeállításával definiálhatjuk.
A Trimble ezen paraméterei, s azoknak a mérések során általam használt é
rtékei a következők:A Silva tételes DGPS mérései esetében ilyen alapbeállításokra nincs lehetőség (a műszer a mért értékeket minősítés nélkül egyszerűen kijelzi), jelentkezik viszont az 3.8.1 fejezetben már említett un. timeout paraméter: azon időintervallum beállítása 10 mp volt.
A hibás tételek nyilvánvalóan szükséges kirekesztésére, egyidejűleg a mért, nyers adatok csökkent megbízhatóságú tételeinek manuális kiszűrésére végül is a következő kritériumrendszert állítottam fel:
A Silva műszer esetében hibás észlelt adatoknak tekinthetőek azon értékek, melyek rögzítésekor az RTCM SC-104 formátum vétele akadályba ütközött, így nem volt valós idejű differenciális korrekció. (hibaüzenet: COLD, AQU vagy noDGPS) Csökkentett megbízhatóságú adatok azok, melyek méréséhez 4-nél kevesebb műhold állt rendelkezésre, vagy a differenciális korrekció a rádióvétel minősége miatt d2 értéknél rosszabb. A 4.1 pontban ismert
etett okok miatt azon adatok is ide tartoznak, melyek rögzítésekor a PDOP érték 6-nál nagyobb volt.A Trimble műszernél hibás tételek nincsenek, mivel a műszer beállításából adódóan, nem megfelelő körülmények között nincs adatrögzítés. Viszont a 6-nál nagy
obb PDOP érték, ugyanúgy csökkentett megbízhatóságú eredményeket von maga után.Az adatsorokban maradtak zavaró elemek. Célom azonban csak az észlelések során tapasztalt legjelentősebb torzítások lokalizálása volt - a minták minden-nemű "befolyásolása" né
lkül.A kizárt tételeket mellőzve a feldolgozás összefoglaló eredményei minden mérési adatsor esetében az alább részletezettek szerint a táblázatok végén találhatóak.
5.3.2 Elsődleges feldolgozás
Az elsődleges feldolgozás során a mérési minták észleléslá
ncolatával két szempontból foglalkozom. Úgy vélem, hogyA 87-4312 EOV számú referenciaponton Silva típusú műszerrel 10 perces észlelés (1 mp-es mintavétel) 473 db értékelhető eredménye alapján, a mérések számtani átlaga Y=472,4081, X=5321,9821 (Gauss-Krüger koordináták). A 3 perces észlelés (5 mp-es mintavétel) 26 értékelhető eredménye alapján Y=472,4110, X=5321,9830. A méréssorozat szélsőértékei közötti különbség a hosszabb észlelés
i idő esetén 20 (Y) ill. 24 m (X), a rövidebb észlelési időt tekintve pedig 15 ill. 20 m. Mindkét esetben az X irányú szélsőértékek nagyobbak az Y irányúaknál.Ugyanezen műszer méréseinek eredményei a 88-3104 EOV számú referenciaponton a következők: A 10 perces észlelés 496 db értékelhető eredménye alapján a számtani átlag Y=473,1691, X=5324,6408, a szélsőértékek közötti különbség 27 ill. 53 m. A 3 perces észlelés 36 értékelhető eredménye alapján Y=473,1696, X=5324,6403, a szélsőértékeket tekintve 20 ill.
20 m. Ezen méréssorozatok szélsőértékeinek eltérése a számtani átlagtól nagyobb, mint a 87-4312 EOV számú referenciaponton vett mérési minták esetében, és a nagyobb X irányú szélsőértékek ugyanúgy jellemzik.A 88-3104 EOV számú referenciaponton Trimble eszk
özzel is történt észlelés, 5 és 2 perces időtartammal, 5 mp-es mintavételezéssel. A 61 db-ból álló mérés-sorozat számtani átlaga szerint Y=768608,102, X=302386,232, a szélsőértékek különbségének nagysága 15,8 ill. 13,2 m. A 24 db eredmény számtani átlaga szerint Y=768607,838, X=302388,135, a szélsőértékek közötti különbség pedig csak 4,9 ill. 1,4 m. A Silva típusú műszer méréseihez hasonlóan a hosszabb mérés - nagyobb elemszámú minta - esetén, a szélsőértékek számtani átlagtól való eltérései nagyobbak, mint a rövidebb méréseknél.Trimble műszerrel végzett észlelések a 87-2419 EOV számú referencia ponton: A hosszabb mérés 57 db eredményének számtani átlaga szerint Y=767614,503, X=304427,570, a rövidebb mérés 23 db eredménye alapján pedig Y=767614,528, X=304429,783. A szélsőértékek közötti különbség 4,2 ill. 10,5 m, valamint 0,7 ill. 1,1 m. A Trimble eszköz által szolgáltatott eredményeknél - különösképpen a 2 perces méréseket tekintve - tapasztalható, hogy kisebb a szélsőértékek közötti különbség, mint a Silva vevő esetében.
A statikus észlelés időtartama alatt a vevőkészülék folyamatosan egy pontban tartózkodik, és közben helymeghatározásokat végez. Ezen helymeghatározások eredményeiben eltérnek egymástól, és az észlelés célja éppen az, hogy a méréssor eredmé
nyeinek átlagát kiszámítva, a mérés végeredményét pontosítsa. A 9. sz. ábra bemutatja azt, hogy a 87-2419 EOV számú referencia ponton, az észlelés ideje alatt miként változtak a helymeghatározás eredményei, ezáltal hogyan vándorolt az adott pillanatban mért pozíció a pont valós helye körül.
9. sz. ábra
Real-time méréseknél igen fontos tényező a differenciális korrekciót hordozó rádióhullámok vételi lehetősége. Rossz minőségű vétel esetén előfordulhat, hogy bizonyos időre megszakad a rádiókapcsolat, és meggátolja a folyamatos differenciális korrekciót. Az újra létrejött kapcsolatot követően rövid ideig a helymeghatározás eredményei nagymértékben eltérhetnek a korábbiaktól. Az 10. sz. ábrán egy részlet látható
a Silva műszer méréséből a 87-4312 EOV számú ponton, pirossal jelölve az értékelésből kizárt tételeket, melyek rögzítésekor nem állt fenn a rádiókapcsolat.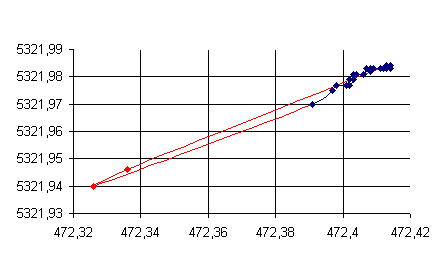
10. sz. ábra
5.3.3 Valószínűségelméleti vizsgálatok
Az elsődleges vizsgálat eredményei hasznosak, egyidejűleg további kérdéseket vetnek fel:
5.3.3.1 Normális eloszlás és paraméterei
A minták behatóbb valószínűségelméleti vizsgálatával a méréssorozat elsődleges, nyers tapasztalatai finomíthatók. Adott statikus méréssorozatban ugyanis észleléseink mindegyik mintaeleme egyazon pont koordinátáinak meghatározására irányul - legjobb akaratunk ellenére hibával terhelten, végül is egymástól eltérő eredménnyel.
Amennyiben kizáró ok nincs, (a méréssorozat alatt a megfigyelés egyéb körülményei változatlanok, azonosak voltak), joggal feltételezhetjük, hogy észleléseink
eredményei, mint valószínűségi változó esetenként csak a mérési adottságok véletlen műveként (mérési háttérzaj, stb.) térnek el egymástól, s ezen véletlen eltérések normális eloszlásúak. Az imént feltett kérdésekre a válasz kiolvasható a minták normális eloszlásfüggvény vizsgálatával, majd pedig az erre alapozott megbízhatóság vizsgálatokkal.A normális eloszlással kapcsolatos matematikai ismereteket [13] alapján az alábbiak szerint foglalom össze:
Egy x
valószínűségi változót normális eloszlásúnak nevezünk, ha sűrűségfüggvénye a következő alakú: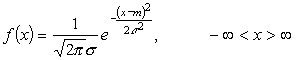
Az eloszlást két paramétere, az m várható érték és a
s szórás egyértelműen meghatározza. A függvény görbe alatti területe, az egész számegyenesen vett integrálja 1-gyel egyenlő. A normális eloszlás az m pontra szimmetrikus, s - alakjáról - haranggörbének is nevezik (11. sz. ábra).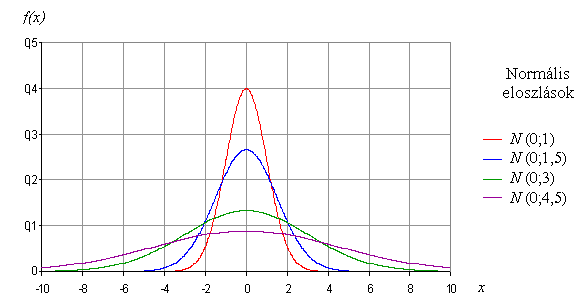
11. sz. ábra
Az m paraméter az x
valószínűségi változó eloszlásának a "centrumát" adja meg, s pedig az eloszlásnak a centrum körüli szóródását hivatott mérni. Nagy s érték szórt, lapos haranggörbét, kis s érték koncentrált, csúcsos eloszlást eredményez. Kitűnik, hogy egy extrém (az átlagostól jelentősen eltérő) mérési érték szakmai súlya, jelentősége, előfordulási valószínűsége csak a s szórás függvényében, ismeretében értékelhető.Az m=0 és
s =1paraméter értékekkel bíró N(0,1) eloszlást standard normális eloszlásnak nevezzük.A normális eloszlás m és
s elméleti értéke egy adott ponton végzett x1,x2, xn n-elemű észleléssorozatból az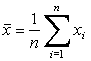
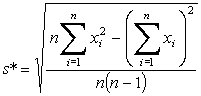
Bizonyítható, hogy a mintaelemszám növekedésével ![]() Ţ m és s*Ţ s . A fenti képlet szerint m legjobb empirikus becslése a számtani átlagérték.
Ţ m és s*Ţ s . A fenti képlet szerint m legjobb empirikus becslése a számtani átlagérték.
5.3.3.2 Megbízhatóság vizsgálat
GPS méréseink - mint minden mintavétel - mindig tartalmaznak kisebb-nagyobb véletlen jellegű hibát. Annak számszerűsítése ezért, hogy az ismeretlen pont koordinátáira munkánk nyomán végül is elfogadott értékben e rejtett hiba mekkora lehet, fontos feladat
.A pontosság k1 és k2
hibahatárai, az un. konfidencia-határok a bemérendő koordináta m várható értékét két oldalról szimmetrikusan fogják közre, távolságuk az általunk választott megbízhatósági szinttől függ. A megbízhatósági szint azon kívánalom, hogy a meghatározandó, ismeretlen koordináta érték az észleléseink alapján kialakított becslés adott (1-p) 100 %-ában (tehát 90% megbízhatósági szint esetén például 100 mérés közül nagy átlagban 90-szer) k1 és k2 közé, a konfidencia-intervallumba essen. Nagyobb megbízhatósági szinthez nagyobb, a kisebbhez kisebb konfidenciasáv tartozik.Általában méréseink nagy megbízhatóságára törekszünk. Észleléseim kiértékeléséhez, az eredmények összehasonlításához én a 80%, 90% és 95% megbízhatósági szinteket választottam.
A mérési eredmények N(m,
s ) eloszlása és ismert s szórás esetén a pont koordinátájára vonatkozó becslésünk hibája az alábbi összefüggés szerint számítható [13]:![]()
![]() +
+![]()
ahol: ![]() az empirikus várható érték
az empirikus várható érték
n a minta elemszáma
up az N(0,1) standard normális eloszlás alapján, adott p>0
esetén meghatározható azon szám, melyre teljesül, hogy

Az up
érték (az integrál felső határa) a választott megbízhatósági szintnek megfelelő p-hez táblázatból kiolvasható. 80% megbízhatósági szintnek p=0,20, 90%-nak p=0,10, 95%-nak p=0,05 felel meg; a hozzájuk tartozó up érték pedig rendre: 1,282, 1,645 és 1,960. (12. sz. ábra)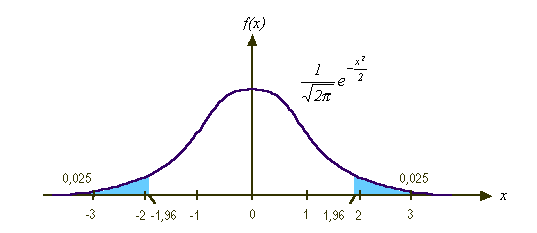
12. sz. ábra
Amint a képletből látható, a méréseink alapján becsült koordinátákat terhelő hiba a megbízhatóság vá
lasztott szintjén csak n-nek, a minta elemszámának, vagyis az adott pontra vonatkozó észleléseink darabszámának függvénye. E tulajdonságból két figyelemre méltó következtetés adódik:1./ Ha a GPS vevővel egy ideig a ponton tartózkodunk, s ott több észlelést is elvégzünk (statikus mérés), a megbízhatóság növelhető, a hiba csökkenthető. A nagyszámú "fölös" mérés a becslésben végül is nagyrészt a pont valódi koordinátáit fogja erősíteni. [4] Ugyanazon megbízhatósági szinten hosszabb észlelési adatsor kisebb,
rövidebb minta nagyobb hibaterhelést eredményez.2./ Szélső esetben a mérés sorozat hossza
n=1 is lehet, mely adott ponton egyszeri, egyetlen észlelést jelent. Ez GPS-mérések esetében gyakran előfordul: mozgó vevő, kinematikus mérés. Látható azonban, hogy a bemért koordinátákban rejlő hiba akkor a legnagyobb, ha becslésünket csak egyetlen észlelésre alapozzuk. Ugyanazon megbízhatósági szinten az eltérés mértéke a statikus méréshez képest akár egy nagyságrend is lehet.Megemlítem, hogy az elemzés fenti konstr
ukciójának megválasztásával egyben némi egyszerűsítéssel élek, miszerint felteszem, hogy a s elméleti szórás ismert és értéke minden statikus méréssorozatnál az abból számítható s* korrigált empirikus szórással azonos. Valójában - mint láttuk - s*=s helyett csak s*Ţ s igaz, és s ismeretlen. Következésképp a becslést a normális eloszlás helyett az un. Student eloszlás alkalmazásával kellene finomítani, melynél az up-hez hasonló funkciójú, jellegű tp szám p mellett még n-nek, a minta elemszámának is függvénye. A Student - vagy t - eloszlás a normális eloszlásból származtatott, ahhoz hasonló habitusú, általános megjelenésű, kinézetű eloszlás. Jellegzetessége, hogy kis n esetén a normális-eloszlástól még kimutathatóan eltér, n növekedésével azonban fokozatosan a normális eloszláshoz simul, s a köztük lévő eltérés n>120 esetén gyakorlati szempontból már elhanyagolható. Mivel ugyanazon p esetén up(p)Ł tp(p,n), az egyszerűsítés végső soron a kimutatható hiba kisebb-nagyobb csökkenését eredményezi.A mérési minták vi
zsgálatánál nem célom a vevőműszerek "tudásbeli" különbségeinek bemutatása, mert egyrészt a felhasználásbeli osztályozáskor az eszközök nem ugyanabba a csoportba esnek, másrészt a műszerekhez tartozó észlelési módszerek is különbözőek, így észrevételeimet csak tényszerűen írom le.A vizsgálathoz segítséget adhat az 13. sz. ábra, mely a korábban részletezett kiértékelés eredményeit ábrázolja, síkban szemlélteti a 88-3104 EOV számú referenciaponton végzett méréssorozatok alapján azt a területet, ahová egyetl
en helymeghatározás eredménye 90 %-os valószínűséggel esik, és azt a becsült területet is, ahol a statikus észlelés végeredménye - számtani átlag - 90 %-os valószínűséggel található.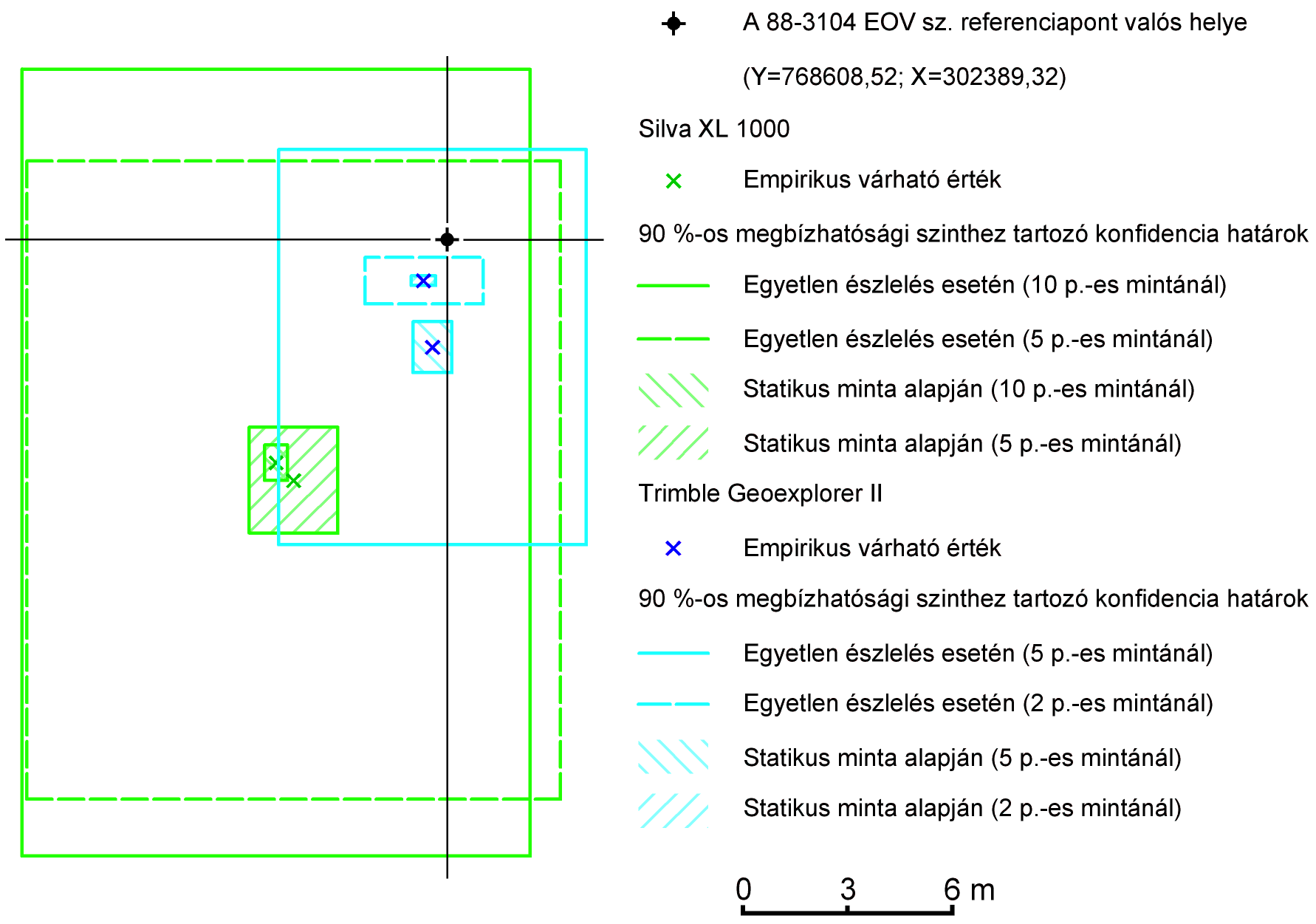
13. sz. ábra
A Silva tí
pusú műszerrel két ponton, összesen 4 db referenciamérést végeztem. Az észlelési minták alapján megállapítható, hogy az értékek szórása 3,7 és 6,9 m közötti, átlagban 4,8 m. Az értékelésnél kiemelem az egyetlen helymeghatározás 90 %-os megbízhatóságához tartozó konfidencia határ és a empirikus várható érték - számtani átlag - közötti távolságot, amely értéke 6,02 és 11,28 m intervallumba esik, átlagos értéke pedig 7,84 m. Mind a négy észlelést tekintve az X irányú konfidencia határ nagyobb az Y irányúnál. A statikus mérések számtani középértékének 90 %-os megbízhatósághoz tartozó konfidencia határa 0,31 és 1,52 m közötti, átlagban 0,85 m.A 10 perces észlelések alaposabb tanulmányozásával az is megállapítható, hogy 5 percet követően a mérés eredménye már nem
javul tovább.A Trimble típusú műszerrel is ugyanúgy 4 db referenciamérést végeztem. A kiértékelés alapján elmondható, hogy a szórásértékek 0,2 és 3,4 m közé esnek, átlaguk 1,3 m. A 90 %-os megbízhatósághoz tartozó konfidencia határok egyetlen helymeghatá
rozás esetén 0,35 és 5,66 m közöttiek, átlagos értékük 2,23 m. A statikus mérések számtani középértékének 90 %-os megbízhatósághoz tartozó konfidencia határa 0,07 és 0,72 m közötti, átlagban 0,32 m.A megbízhatóság vizsgálat említett mutatói szerint úgy tűnhet, mintha a 2 perces mérések megbízhatóbbak lennének, mint az 5 percesek, azonban ez valószínűleg csak a szerencsésen kiválasztott 2 perces időintervallumoknak köszönhető.
5.3.4 A mérési eredmények a referenciapontok adatainak tükrében
A tárgyalt vizsgálatok hasznosnak bizonyulnak a műszerek tulajdonságainak, jellemzőinek megismeréséhez, alapot adnak azok típusának megválasztásához, képességeik összehasonlításához, másfelől támpontot nyújtanak az alkalmas mérési módszerek kialakításához.
A felhasználót a
megbízhatóságra utaló, említett relatív jellemzők mellett azonban leginkább az elérhető abszolút pontosság foglalkoztatja. A műszerek felépítésének belső "titkaiból" és a különböző mérési módszerekből összeálló bonyolult kombináció miértjén, hogyanján túl, végső fokon az a leglényegesebb, hogy a referenciapontok korábban már nagy pontossággal meghatározott, ismert koordinátáinak reprodukálása tekintetében a rendszer miként vizsgázik.A referenciapontokon végzett statikus észlelések alapján a koordinátákra kialakítható becslés és a referenciapont valós helye közötti eltérést az alábbi táblázatban foglalom össze.
|
Mérés helye |
Műszer |
Észlelés jellemzői |
D Y [m] |
D X [m] |
|
87-4213 |
Silva |
10 perc, 1 mp mintavétel |
-7,1 |
-4,5 |
|
|
Silva |
3 perc, 5 mp mintavétel |
-4,2 |
-3,6 |
|
88-3104 |
Silva |
10 perc, 1 mp mintavétel |
-4,9 |
-6,4 |
|
|
Silva |
3 perc, 5 mp mintavétel |
-4,4 |
-6,9 |
|
|
Trimble |
5 perc, 5 mp mintavétel |
-0,7 |
-3,1 |
|
|
Trimble |
2 perc, 5 mp mintavétel |
-0,4 |
-1,2 |
|
87-2419 |
Trimble |
5 perc, 5 mp mintavétel |
-0,9 |
0,4 |
|
|
Trimble |
2 perc, 5 mp mintavétel |
0,9 |
1,7 |