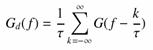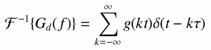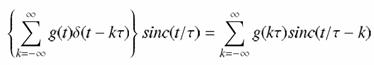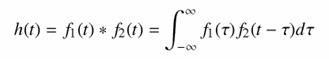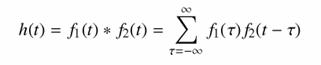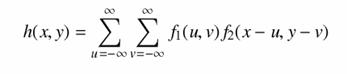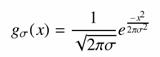Tartalomjegyzék
A mintavételi tétel néhány kÖvetkezménye
AutomatizÁlt domborzat generalizÁlÁs
SŰrŰ És ritka domborzati rÁcsok
Az automatikus raszter-vektor konverziÓ lehetŐsÉgÉrŐl
Ami egyelŐre nem vÁrhatÓ az automatikus raszter-vektor konverziÓs eljÁrÁstÓl
ElŐfeldolgozÓ workflowk És tudÁsbÁzisok tervezett elŐÁllÍtÁsa
Az IRIS csomag alkalmazÁsa ŰrfelvÉtelekre
fraktÁlgeometria a fÖldtudomÁnyban
A Sierpinsky-szŐnyeg És a Menger-szivacs
Domborzati problémák
A digitális domborzati modellekkel operáló szoftverek előszeretettel használnak szabályos rácsban tárolt magassági adatokat. Ez a forma egyszerű, úgy a megjelenítés, mint a számolások számára kézenfekvő. Ezt a modellt vizsgáljuk meg a jelfeldolgozásban jól ismert mintavételi tétel szempontjából.
Először vázlatosan áttekintjük a mintavételezés folyamatát, majd ismertetünk néhány következtetést.
Mintavételezés
A szaktudományokban alapvető jelentőségű az adatnyerés folyamata, amely a technika mai szinvonalán digitális adatnyerést vagy mintavételezést jelent. Mintavételezéskor gyakran analóg jelekből állítunk elő digitális adatokat, máskor eleve diszkrét, esetleg nem szabályosan elhelyezkedő mintavételi pontokban történik az adatnyerés. A mintavételezés folyamatának megértése nagy jelentőségű, mivel az adatokból levonható következtetések függhetnek a mintavételezés módjától.
Képzeljük el a mintavételezést, mint egy kétállású kapcsolóval szabályozott mérő berendezést, amely bekapcsolt állapotban rögzíti a mérendő paramétert, kikapcsolt állapotban pedig mit sem tud a környezetéről. Más szavakkal azt is mondhatjuk, hogy két mintavételi (idő)pont között bármi történik is, arról nem fogunk tudomást szerezni, mivel mérő berendezésünk ilyenkor kikapcsolt állapotban van. Belátható, hogy ez a fajta hiányosság csökkenthető, ha sűrítjük a mintavétel gyakoriságát, vagyis csökkentjük az érzékelés nélkül töltött üzemmód részarányát a működő állapothoz képest. Nevezzük mintavételi távolságnak két érzékelés közötti intervallumot, amely, ha idősorokról van szó akkor idő dimenziójú, de lehet távolság dimenziójú is, ha két mintavételi pont között térbeli távolságról van szó.
A következőkben vázlatosan áttekintjük a mintavételezés legfontosabb törvényszerűségeit, egyenletes mintavételezést feltételező esetekben. Az egyszerűség kedvéért idősorokkal, vagyis egy dimenziós problémákkal foglalkozunk, amik teljes mértékben általánosíthatók több dimenziós esetekre is, mint amilyenek a terepmodellek.
Mintavételi tétel
Legyen t az úgynevezett mintavételi távolság. Ábrázoljuk a g(t) időfüggvényt és a mintavételezés eszközét, a Dirac impulzusok sorozatát, majd a mintavételezés eredményét, a digitalizált időfüggvényt (1. ábra).
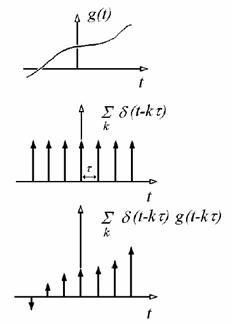
1. ábra
Az analóg függvény, a Dirac impulzus sorozat és a digitalizált jel.
A mintavételezés eredménye egy olyan impulzus sorozat, melynek tagjai az eredeti függvénynek a mintavételi helyeken felvett értékei.
A mintavételezés tehát nem más, mint a g(t) időfüggvény és a Dirac impulzus sorozat szorzata:
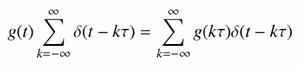
Vizsgáljuk meg az analóg függvény és a mintavételezett spektrumát. Jelöljük G(f)-fel az eredeti, és Gd(f)-fel a digitalizált függvény spektrumát. A Dirac-d Fourier-transzformáltjának és a konvolúció tételek felhasználásával felírható a mintavételezett függvény spektruma:
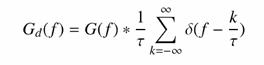
vagyis
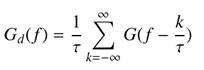
Értelmezzük a kapott eredményt. A kifejezés jobb oldala szerint a digitalizált jel spektruma periodikus, ami azért érdekes, mert aperiodikus függvények (vagy más néven tranziens függvények) spektruma nem periodikus függvény, vagyis a mintavételezés az eredetileg nem periodikus spektrumot periodikussá teszi. A spektrumnak a -½t és ½t közé eső részét a spektrum fő részének, az fN = ½t értéket Nyquist-frekvenciának nevezzük. A spektrum többi részén a fő rész fN periódussal ismétlődik. A fenti formulákból világosan kiolvasható, hogy az analóg és a digitalizált függvény spektruma jelentősen eltérhet egymástól, ha az analóg függvény tetszőleges frekvenciájú jeleket is tartalmazhat. Ha azonban létezik egy olyan felső határfrekvencia (ff), amelynél nagyobb frekvenciájú jel nem fordulhat elő (vagyis létezik a spektrumra felső határfrekvencia), akkor belátható, hogy a felső határfrekvencia és a t mintavételi távolsággal még átvihető legnagyobb frekvencia között igaz a következő összefüggés:
ff <= fN
vagyis
t <= 1/(2 ff)
Ez az összefüggés a mintavételi tétel. Jelentése, hogy mintavételezéskor a még átvihető legnagyobb frekvenciához, ff -hez úgy kell megválasztanunk a mintavételi távolságot (t), hogy teljesüljön a mintavételi tétel. Ha ennél kisebbre választjuk a mintavételi távolságot, akkor feleslegesen sűrűn mintavételezett adatrendszert kapunk, ha pedig ennél nagyobbra választjuk, akkor nem fog teljesülni az ff felső határfrekvencia szerinti jelátvitel. Túlzottan ritka mintavételezéssel tehát felülvágást fogunk végrehajtani az adatrendszer spektrumán.
A mintavételi tétel néhány következménye
Láthattuk, hogy bizonyos esetekben a digitalizálás (mintavételezés) adatvesztéssel járhat. Tekintsük át, hogy mikor nem vesztünk adatot (mikor veszünk észre mindent). A megfelelően mintavételezett digitális adatrendszerből az eredeti analóg jel (jelen esetben a felszín) pontosan visszaállítható. Akkor mondjuk megfelelően mintavételezettnek az adatrendszert, ha teljesült a mintavételi tétel. Az előző részben láthattuk, hogy a mintavételezés periodikussá teszi a spektrumot. Ha pontosan vissza kívánjuk állítani az eredeti analóg jelet a mintavételezett jel spektrumából (Gd(f)), akkor el kell tüntetnünk a spektrum fő részein kívüli részeit, vagyis meg kell szoroznunk Gd(f)-t egy olyan négyszög függvénnyel, amelynek magassága t, szélessége 1/t. Így egyszerűen levágjuk a spektrum periodikus részeit, vagyis kiküszöböljük a mintavételezéssel belevitt periodicitást, vagyis visszakapjuk az analóg jel spektrumát.
Az ismertetett gondolatmenet akkor adja vissza a jelet az idő tartományban, ha a visszakapott spektrumot inverz Fourier-transzformáljuk. Ismerve a konvolúció tulajdonságait és a négyszög-függvény (inverz) Fourier-transzformáltját, belátható, hogy a t magasságú és 1/t szélességű négyszögfüggvénnyel való szorzás a frekvencia tartományban a sinc függvénnyel való konvolúciót jelent az időtartományban. Ez alapján a jel visszaállítása az időtartományban a következő módon lehetséges:
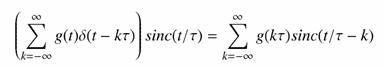
vagyis a visszaállított értékek a minták és a sinc függvény megfelelő argumentummal vett értékeinek szorzatai. Ez egyrészt azt jelenti, hogy az így visszakapott értékek pontosan azonosak az egyes minták értékeivel, valamint az analóg függvény tetszőleges helyén felvett értékek előállíthatók a mintáknak és a megfelelő argumentummal megadott sinc függvényértékek szorzatának összegzésével. Természetesen csak akkor igazak ezek a megállapítások, ha teljesült a mintavételi tétel. Túl nagyra választott mintavételi távolság esetén az analóg jel spektruma nem állítható vissza pontosan, mivel a túl ritka mintavétel felülvágást hajtott végre a spektrumban.
Domborzati modellek
A domborzati modellek megalkotásának egyik fontos állomása, hogy ismerjük szabályos rácspontokban a felszíni magasság értékeket. Ezen adatnyerési technikák ismertetését mellőznénk, ugyanakkor fontosnak tartjuk kiemelni a mintavételi tétel ide vonatkozó következményeit. A magasság értékek egy a felszínt leíró analóg függvénynek egy t rácsállandójú Dirac impulzus sorozattal való szorzásával kaphatók meg (2. ábra)
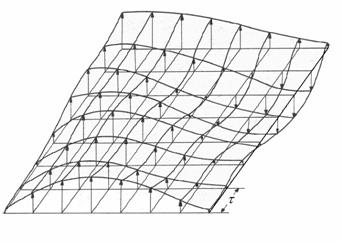
2. ábra
A t rácsállandójú Dirac-d sorozattal mintavételezett felszín
Ebből kézenfekvően adódik, hogy a t hosszúságú mintavételezéssel nem tudunk kimutatni 2t-nál kisebb méretű terepi képződményeket.
A 3. ábrán egy valóságos domborzati modellt láthatunk, amelynek felbontóképessége kb. 5m, amivel a mintavételi tétel miatt 10 m-nél kisebb horizontális kiterjedésű felszíni egyenetlenség nem mutatható ki. Ezért csak építészeti, várostervezési célú felhasználása javasolt. Ha például a felhőszakadások alkalmával lezúduló csapadékvíz lefolyását kívánnánk modellezni, akkor pontosabb (kisebb mintavételi távolságú) domborzati modellt kellene megalkotni.
Ha mindezt árvízveszélyes területre vonatkoztatjuk, akkor belátható, hogy egy a fenti pontosságnak eleget tevő magassági modell két mintavételi pontja között mit sem tudunk a terep alakulásáról. Így az árvízvédelmi töltésen, két, egymástól 10 méterre lévő mintavételi pont között nem fogjuk tudni megmondani, hogy ott milyen magassági értékek vannak, márpedig ez nem engedhető meg. Erre a célra sokkal sűrűbben mintavételezett magassági modell kell.
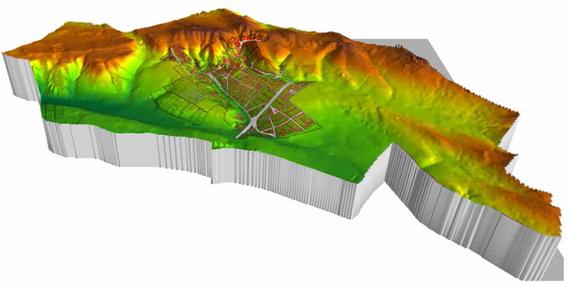
3. ábra
Egy domborzati modell perspektivikus megjelenése.
A település digitális térképe rá van feszítve a felszínre.
Általánosságban kimondható, hogy nincsenek univerzálisan, minden célra alkalmas domborzati modellek. A pontossággal szembeni elvárások eltérő mivolta egyben különböző mintavételezési kritériumokat is jelent. Ezért fordulhat elő, hogy ami a telekommunikáció számára megfelelően pontos domborzati modell, az árvízvédelem számára nem az.
Automatizált domborzat generalizálás
Egy előző cikkben ismertettünk a domborzati modellekre vonatkozóan a mintavételi tételből következő néhány megállapítást. Most bemutatunk egy az adatrendszerek ritkításán alapuló automatikus generalizálási eljárást. A ritkítás, ha a mintavételi tételre figyelemmel végezzük, olyan szabályozott körülmények közötti, kontrolált adatvesztést valósít meg, ami nagyon hasonlatos a térképészetben használt generalizálásra. A bemutatott technika egyelőre csak domborzatra lett kidolgozva.
A cikk első részében bemutattuk a mintavételezés folyamatát, matematikai modelljét és a mintavételi tételt. A következőkben megvizsgáljuk a mintavételezés átviteli tulajdonságait annak érdekében, hogy megértsük a ritkítás hatását.
Az analóg jel visszaállítása
Mint az előző cikkben említettük a mintavételezéssel egy digitális adatrendszert állítunk elő egy folytonos függvényből, a mintavételi tétel figyelembe vételével. A mintavételi tétel betartásával biztosítható, hogy a digitális adatrendszer és analóg függvény spektruma megegyezzen, ezáltal biztosítva a veszteségmentességet.
Csak emlékeztetőképpen idézzük vissza az előző cikk néhány fontos megállapítását.
Jelöljük G(f)-fel az eredeti, és Gd(f)-fel a digitalizált függvény spektrumát. A Dirac-d Fourier-transzformáltjának és a konvolúció tételek felhasználásával felírható a mintavételezett függvény spektruma:
|
vagyis
|
A kifejezés jobb oldala szerint a digitalizált jel spektruma periodikus, ami azért érdekes, mert aperiodikus, folytonos függvények spektruma (vagyis az analóg adatrendszeré) nem periodikus függvény, vagyis a mintavételezés az eredetileg nem periodikus spektrumot periodikussá tette. A spektrumnak a -½t és ½t közé eső részét a spektrum fő részének, az fN = ½t értéket Nyquist-frekvenciának nevezzük. A spektrum többi részén a fő rész fN periódussal ismétlődik.
A mintavételezés tehát megváltoztatta a digitális adatrendszer spektrumát az analóg jel spektrumához képest. Ha azt akarjuk, hogy a digitalizálás adatvesztés nélkül reprezentálhassa az analóg adatrendszert, akkor azonossá kell tenni a spektrumokat. Ezt úgy érhetjük el, hogy levágjuk a digitális adatrendszer Nyquist-intervallumán kívül eső spektrum részeket. Ez a művelet egy t magasságú és 1/t szélességű négyszögimpulzussal való szorzást jelent. Jelölje £ a négyszögfüggvényt. Ekkor a spektrumismétlődést megszüntető levágásra írható, hogy
|
Így elértük, hogy az analóg és a digitális adatrendszer spektruma azonos lesz, amely egyben azt is jelenti, hogy a digitális adatrendszerből adatvesztés nélkül visszaállítható az analóg adatrendszer.
A mintavételezés azonban az időtartományban történik, ezért meg kell értenünk azt is, hogy az amúgy meglehetősen egyszerű művelet a frekvencia tartományban – mármint a spektrum fő részén kívüli tartomány levágása –mit jelent az időtartományban. A digitalizált adatrendszer levágott spektrumának inverz Fourier-transzformációjával
|
valamint annak figyelembe vételével, hogy
|
A konvolúció-tétel alkalmazásával kapjuk
|
vagyis a visszaállított analóg függvényt a mintákkal szorzott sinc függvények összegeként kapjuk meg.
Átmintavételezés
Előfordulhat, hogy valamely okból egy létező adatrendszert egy másik mintavételi távolságra áttérve szeretnénk átalakítani. Ha csökkentjük a mintavételi távolságot, akkor sűrítést, ha növeljük, akkor ritkítást hajtunk végre. A sűrítés – amit gyakran interpolációnak is nevezünk – nem változtatja meg az adatrendszer spektrumát, de a ritkítás igen. A cikkben tárgyalt probléma szempontjából a ritkítás az érdekes, tehát most csak ennek hatásait igyekszünk áttekinteni.
Legyen te az eredeti és tr a ritkított adatrendszer mintavételi távolságai. Mint tudjuk az átvihető legnagyobb frekvencia (ffe ) és a mintavételi távolság (te ) között fennáll a következő összefüggés:
te < 1 / 2ffe |
ami a ritkítás után is igaz, csakhogy egy másik felső határfekvenciára, a ritkítás utánira (ffr)
tr < 1 / 2 ffr |
A ritkítás utáni spektrumból az ffe és az ffr közötti frekvenciasáv hiányozni fog, mégpedig az 4. ábrán látható módon:
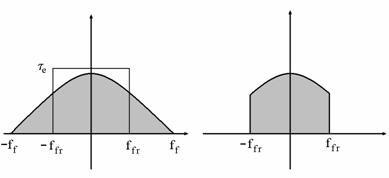
4. ábra
Az ábra bal oldali részén a ritkítás előtti, a jobb oldali részén a ritkítás utáni spektrumot láthatjuk. ffe az eredeti adatrendszer felső határfrekvenciája, ffr a ritkítás utánié. A levágást egy 2 ffr (azaz 1/tr ) hosszúságú és te magasságú négyszögfüggvénnyel végeztük.
A ritkítás végrehajtását az utóbbi formulák alkalmazásával értük el, vagyis a ritkított függvényt az eredeti mintákkal szorzott sinc függvények összegeként kaptuk meg.
Sűrű és ritka domborzati rácsok
Tekintsük meg a 5. ábrát, amin egy sűrűn mintavételezett magassági modellt láthatunk perspektivikusan ábrázolva. A 6. ábrán az előbbi terület rétegszínezéses térképét láthatjuk.
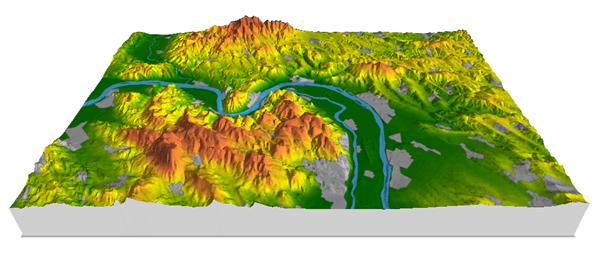
5. ábra
Az eredeti adatrendszer 3 dimenziós, perspektivikus megjelenítéssel. A mintavételi távolság 50m.

6. ábra
Az eredeti adatrendszer rétegszínezéses megjelenítéssel. A mintavételi távolság 50m.
Hajtsunk végre erőteljes adatritkítást a szabályos rácsban rendelkezésre álló magassági adatbázison. Növeljük például 10 szeresére a mintavételi távolságot. A mintavételi tételből tudjuk, hogy ezáltal el fogjuk veszíteni a jel spektrumából az 1/2t-nál nagyobb frekvenciákat, vagyis simító szűrést hajtunk végre az adatrendszeren, ezáltal el fognak tűnni a domborzatból a gyors változások, kisebb kiterjedésű egyenetlenségek. Amikor hagyományos módon generalizál a térképész, pontosan ilyen műveletet hajt végre.
A 7. ábra a ritkított adatrendszerből számított magassági modellt mutatja perspektivikusan, míg az 8. ábra ugyanezt rétegszínezéssel ábrázolva.
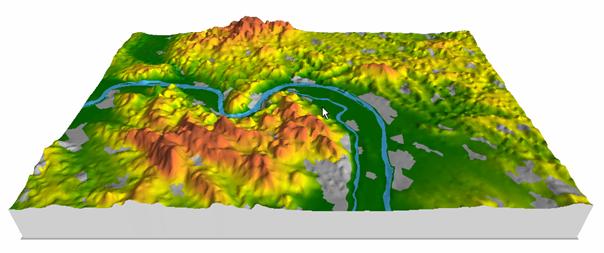
7. ábra
A ritkított adatrendszer 3 dimenziós, perspektivikus megjelenítéssel. A mintavételi távolság 500m.

8. ábra
A ritkított adatrendszer rétegszínezéses megjelenítéssel. A mintavételi távolság 500m.
A ritkítás által egy olyan eljáráshoz juthatunk, amely a generalizálást nem szubjektív ismérvek alapján végzi el, hanem a fizikai felfogásunkhoz legközelebb álló, automatikus módon, tehát mindig ugyanúgy, reprodukálhatóan.
Az ismertetett eljárásra írt programok egyelőre kísérleti jellegűek. Ahhoz, hogy technologizált módon működjenek, még számos szoftverkonstrukciós részletkérdést kell megoldani, amik azonban nem érintik a módszer lényegét.
A magassági modelleket Intergraph Geomediával jelenítettük meg. A magassági modell alapját az MHTÉHI DDM-50 nevű digitális domborzat modell adatállománya képezte.
Felhasznált irodalom
1. M. Bellanger: "Digital Processing of Signals, Theory and Practice", John Wiley and Sons, 1986
2. S. Smith: "Digital Signal Processing", Elsevier Science, 2003
3. R.Longley-M.Goodchild-D.Maguire-D.Rhind:"Geographic Information, Systems and Sciense", Wiley, 2002
4. Klinghammer – Papp-Váry: „Földünk tükre a térkép”, 1983, Gondolat, Budapest
5. Meskó A.: "A digitális szeizmikus feldolgozás alapjai", Tankönyvkiadó, Budapest, 1975
6. Meskó A.: "Geofizikai adatfeldolgozás I., lineáris átalakítások", Tankönyvkiadó, Budapest, 1983
7. J. F. Richards: "Remote sensing Digital image analysis", Springer-Verlag, 1986, Australia
8. J. Duncan: "Bevezetés a komplex függvénytanba", Műszaki könyvkiadó, Budapest, 1974
9. R. Cristescu - G. Marinescu: "Bevezetés a disztribúció elméletbe", Műszaki könyvkiadó, Budapest, 1969
Az automatikus raszter-vektor konverzió lehetőségéről
A térkép digitalizálás régóta áhított technológiája az automatikus raszter-vektor konverzió. Számos próbálkozás történt már a probléma megoldására, nemcsak a geoinformatika, hanem egyéb grafikus alkalmazások területén is. Több-kevesebb sikert mindenki fel tudott mutatni, de kifogástalan működést egy sem (az általam ismert implementációk közül). Csak egészen speciális esetekben (pl. csak szintvonalakat tartalmazó fedvények) lehetett jó minőségűnek mondani az előállt vektoros állományt. Általában alig lettek használhatók az előállt adatproduktumok.
A legtöbb konverziós eljárás valamiféle vonalkövetést próbált megvalósítani, amikor is azonos vagy hasonló intenzitású, színű pixelek által jelölte ki a leendő vektoros állomány nyomvonalát. Az elképzelés első ránézésre akár működőképesnek is vélhető, sajnos azonban a legtöbb gyakorlati esetben nagyon rossz minőségű lett a kapott vektoros anyag, amely csak jelentős utólagos emberi beavatkozás után vált használhatóvá. Igen sok esetben kétséges volt, hogy vajon nem egyszerűbb-e a rosszul működő automatikus konverzió helyett a lassabban, de kvázi hibátlanul dolgozó emberrel végeztetni el a munkát. A válasz sokszor az emberi munka mellett döntött, különösen olyan országokban, ahol olcsón áll rendelkezésre képzett munkaerő. Fejlettebb implementációk jelentős interaktivitást is megengedtek a szoftvert működtető embernek. Ezzel mindenképpen gyorsult a vektorizálási eljárás, lényegesen javult a kapott vektoros anyag minősége, de állandó emberi jelenlétet és döntést igényelt.
A következőkben megvizsgáljuk egy nem a vonalkövetés elvén alapuló raszter-vektor konverziós eljárás elvi és gyakorlati működését. A neve IRIS, az angol Intelligent Rasterimage Interpretation System szavak kezdőbetűiből származik. Az ELTE Informatikai Karán működő Informatikai Kooperatív Kutatási Központ (IKKK) és az MTA Térképtudományi és Térinformatikai Kutató Csoportjának egyik kiemelt kutatási témája.
Elvi megfontolások
Először is vizsgáljuk meg a látás pszichológiájából származó tapasztalatokat, tekintsük át a szempontokat, amiket a térképet olvasó ember figyelembe vesz. Gaetano Kanizsa [1] óta tudjuk, hogy a szem éleket detektál, amik révén szegmentálja a nézett képet. Az élek detektálása után „szemrevételezi” az élek közötti foltokat, vagyis poligonokat értékel ki. Az éldetektálás különös esetei az éltalálkozások, sarkok, szögletek, amelyek többnyire valamilyen speciális szituációt jeleznek (intelligens, a látást szimuláló gépek esetében a szögletek alkalmasak lehetnek a tárgyak térbeli helyzetének, egymás fedésének, takarásának megállapítására, míg térképek esetében a vonaltalálkozások szintén kritikus pontjai a térkép kiértékelésének, olvasásának).
A tapasztalat azt mutatja, hogy látásunk nagy megbízhatósággal képes kiértékelni a térképen látható vonalak és foltok rendszerét. Ennek oka két fő csoportban keresendő.
Egyrészt a szemünk képfeldolgozó képessége rendkívüli. Kiváló éldetektor. Megbízhatóan szegmentál. Felületként értelmezi az élek közötti területet. Ezek a képességek – bármennyire hasznosak is – csak előkészítik a terepet a képek tényleges értelmezéséhez, például a térkép „olvasásához”, egy arc, egy ujjlenyomat felismeréséhez.
Másrészt mit jelent az a kifejezés, hogy valaki „olvasni” tudja térképet? Mindenekelőtt azt, hogy ismeri a térképkészítés, a felszínábrázolás konvencióit, a térkép jelkulcsát, rendelkezik azzal az ismeretanyaggal, ami által felismeri, hogy a térképen látott helyzet milyen valóságos állapotot szimbolizál. Ha tehát egy gépet (computert) meg akarunk tanítani a térképek olvasására, akkor mindenek előtt fel kell ruháznunk a térképet olvasni képes ember tudásával. Ez egyrészt annyit jelent, hogy képessé kell tenni a gépünket a tudás tárolására, olyan elemi tudásrészek révén, amiből saját tudásunk is felépül, másrészt hatékony keresési algoritmusokkal kell, hogy felruházzuk annak érdekében, hogy gyorsan hozzáférjen a szükséges tudáshoz.
A fenti megállapításokból számos következmény ered. Biztosra vehető, hogy a tudás más kell legyen az egyes térképfajták számára (mint például kataszteri, topográfiai térképek). Más kell legyen az egyes országok térképei számára is, hiszen a jelkulcsok nem egységesek a világban, sőt különböző konvenciók létezhetnek országról országra. Elképzelhető, hogy egyes térképészeti iskolák, akár egy országon belül is, más tudásbázist igényelnek. Világosan látnunk kell, hogy csak akkor várhatunk hibátlan működést a térképolvasó gépünktől, ha az ahhoz legjobban megfelelő tudásbázis használjuk
Az alkalmazott eljárások
Ez után az elvi áttekintés után vizsgáljuk meg a részleteket. Vegyük először az előfeldolgozásnak nevezett eljárás-csoportot.
Előfeldolgozás
Előfeldolgozás alatt azon eljárások gyűjteményét értjük, amit még azelőtt használunk, mielőtt a tudásbázishoz fordulnánk, vagyis mielőtt bármilyen gépi intelligenciát vetnénk be. Az előfeldolgozás két fő eljárás-csoportól áll: az egyik a képelőkészítés, a másik a nyers vektorizálás. Terjedelmi korlátok okán csak a legfontosabb képelőkészítő eljárásokat tekintjük át.
Képelőkészítés
o Canney-féle éldetektor
o Medián szűrő
o Zaj és frekvencia szerinti szűrések (Alul és felülvágók, sávszűrők)
o Szín műveletek (szín szerinti leválogatás, színcsere, kivonás, stb.)
o Szegmentáló eljárások
Ezek közül néhányat vizsgáljunk meg egy kicsit behatóbban, hogy lássuk mekkora hatékonysággal tisztul le általuk a kezdetben igencsak változatos kép.
Mielőtt áttekintenénk a legfontosabb képelőkészítő eljárásokat, foglaljuk össze a konvolúció fogalmát, amely a képfeldolgozásban nagyon fontos szerepet játszik.
Az egyszerűség kedvéért nézzünk először csak az egydimenziós esetet. Legyenek f1 és f2 folytonos függvények. Jelölje konvolúciójukat h = f1 * f2, melyet a következő kifejezés definiál:
|
Az 9. ábra grafikusan szemlélteti két négyszög függvény konvolúcióját:
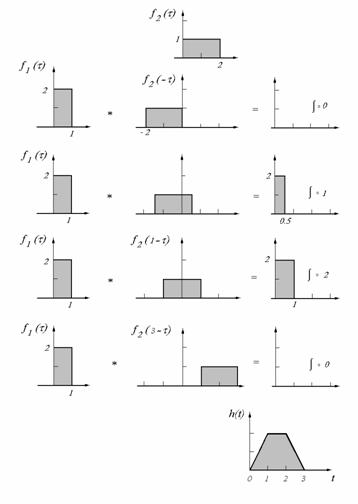
9. ábra
Két négyszög függvény konvolúciója
Digitális jelekre alkalmazva az összefüggést:
|
Vizsgáljuk meg egy konkrét esetet: Legyen h(t) a t-edik pillanatban az f1 és f2 függvények konvolúciója, amit úgy kapunk, hogy az f1 t-edik pillanatban felvett értékét összeszorzunk az f2 (t-t) -edik értékével, majd végigfutunk f2 egész intervallumán (ami valóságos esetekben véges intervallum, jelen esetben M) és összegezzük a szorzatokat (futó összegzés). A folyamatot a 10. ábra szemlélteti.
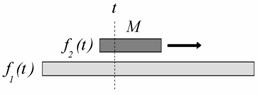
10. ábra
A konvolúció szemléletes jelentése
Az eddigiekben csak egydimenziós függvényekkel foglalkoztunk. Könnyen általánosítható a konvolúció fogalma kétdimenziós függvényekre is, mint amilyen a digitális kép.
|
A digitális szűrési módszerek egyik legfontosabb fogalma a kernel. Jelentése mag. A szűrési eljárások, amikor az időtartományban dolgoznak, a kernellel konvolválják a szűrendő képet. A szűrés hatása attól függ, hogy milyen függvény értékeit tesszük be a kernelbe, ami egy n*n méretű táblázat (n a szűrő hossza). Ha meg tudjuk adni, hogy milyen átviteli függvényt kívánunk megvalósítani a frekvencia tartományban, akkor annak inverz Fourier-transzformálásával megkapjuk az időtartománybeli függvényt, amelyet megfelelően mintavételezve megkapjuk a szűrőegyütthatókat, vagyis a kernelbe töltendő számokat.
A digitális konvolúció tehát a szűrések végrehajtásának egyik lehetséges módja. Ebben az esetben a szűrést az időtartományban végezzük a következő módon:
g'(t)= g(t) * s(t)
ahol g(t) az eredeti adatrendszer az időtartományban, g'(t) a szűrt adatrendszer és s(t) a kernel.
Egy másik lehetséges megoldás, hogy a szűrendő adatrendszert Fourier-transzformáljuk, majd a frekvencia tartományban végezzük el a szűrést (a Fourier-transzformáltat megszorozzuk a kívánt hatást biztosító átviteli függvénnyel), majd az így kapott spektrumot inverz Fourier-transzformáljuk.
G(f)= F { g(t) }
G'(f) = G(f) S(f)
g'(t)= F -1 { G'(f) }
ahol g(t) az eredeti adatrendszer, G(f) az adatrendszer Fourier-transzformáltja, S(f) a kívánt átviteli függvény, G'(f) a szűrt adatrendszer a frekvencia tartományban, g'(t) a szűrt adatrendszer az időtartományban, F a direkt, és F-1 az inverz Fourier-transzformációt szimbolizálja.
A kernel megállapítása nemcsak a frekvencia szerinti szűrők esetén játszik kulcs fontosságú szerepet, hanem más egyéb esetekben is, mint például az élmegőrző, élkiemelő szűrők. Az elérendő cél néha olyan, hogy nem adható meg egy egyszerű átviteli függvénnyel a művelet, hiszen pontról pontra változhat az algoritmus által előírt tennivaló. Ilyenek az éldetektorok, élmegőrzők, a kép deriválók, stb.
Nézzük meg részletesen, hogy mi is történik a kernel és a kép konvolúciójakor. Vegyünk például egy 3*3 pixel méretű kernelt (11. ábra). Egyelőre fogadjuk el, hogy valamilyen számokkal fel van töltve a kernel.

11. ábra
Az erősen felnagyított kernel mozgása egy képen
A kernellel pixelenként végigfutunk a képen a 11. ábrán látható módon.
Helyezzük rá a kernelt a képre (mondjuk a bal felső sarokba). A sötét mező nyilván valamelyik pixelre fog esni. A kernel közepén lévő sötét mező kitüntetett szerepű, mivel a kernel hatása mindig arra a pixelre vonatkozik, ami fölött a kernel középpontja áll. A kernel hatása a sötét mező alatti pixelre a következőképpen állapítható meg:
1. A kernel első mezőjében lévő számot szorozzuk meg az alatta lévő pixel színével (RGB szín), majd tároljuk az eredményt.
2. Vegyük a kernel második mezőjében lévő számot és szorozzuk meg az alatta lévő pixel színével, majd az így kapott számot adjuk hozzá az előző eredményhez.
.
.
.
5. Vegyük a kernel ötödik (sötét) mezőjében lévő számot és szorozzuk meg az alatta lévő pixel színével, majd az így kapott számot adjuk hozzá az előzőek eredményéhez.
.
.
.
9.
Minden szorzatot hozzáadtunk az előzőhöz, majd az összeget elosztottuk 9-cel (vagy annyival, ahány elemű a kernel), ami egyébként a szűrés eredménye is, vagyis a sötét mező alatti pixel szűrt értéke. A művelet eredménye csak egyetlen pixelnek a szűrt színe. Az egész kép szűréséhez mindezt annyiszor kell végrehajtani, ahány pixeles a kép.
Canney-féle éldetektor
Az éldetektálás különösen fontos szerepet játszik az alakfelismerésben, a raszteres térképek vektorossá alakításában. Az élek a képnek azon helyei, ahol az intenzitás megváltozása a legnagyobb. Először is döntsük el, hogy mennyire kifinomult élek kimutatását szeretnénk. A legtöbbször érdemes simító vagy medián szűrésnek alávetni a képet, hogy ne mutassunk ki minden apró, jelentéktelen élt. Egyik ismert és egyszerű módja a simításnak a kép és egy Gauss-függvény konvolúciója:
|
Legyen h az f és g függvények konvolúciója. Kimutatható, hogy
h = (f * g)’ = f * g’ |
vagyis egy jel (jelöljük f-el) Gauss-függvénnyel (g) való konvolúciójának a deriváltja egyenlő a jel és a Gauss-függvény deriváltjának a konvolúciójával. Ezek alapján az éldetektálás algoritmusa a következő:
1. Konvolváljuk f -t g' –vel
2. Számítsuk ki h abszolút értékét
3. Definiáljuk éleknek mindazokat a helyeket, ahol a h abszolút értéke meghalad egy előre meghatározott küszöb értéket. }
Nem használtuk ki sehol a gondolatmenet során, hogy egy vagy kétdimenziós esettel van-e dolgunk, így az éldetektálás fenti módja képek esetére is működőképes. Ez az eljárás a Canny-féle éldetektor. Eredménye a 12. ábrán látható egy szintetkus test példáján.
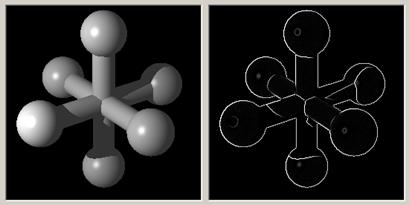
12. ábra
Az éldetektálás tárgya (bal oldali ábra) és eredménye (a derivált, jobb oldali ábra). A jobb oldali ábra olyan, mintha vektoros lenne, pedig nem az. Egy végletekig letisztult kép deriválása révén kapott képre már a nyers vektorizálás is jó eredményt adhat.
Medián-szűrő
Az élmegőrző rangszűrők olyan speciális szűrők, amelyek átviteli függvényei nem adhatók meg. Működésük meglehetősen egyszerű algoritmus szerint történik. A kernelt mozgassuk végig a képen, és töltsük fel az éppen alatta lévő pixelek értékeivel. Rendezzük nagyság szerint sorba a kernel elemeit, és a rendezett adatsor valamelyik elemét rendeljük hozzá a kernel szimmetria középpontja alatt lévő pixelhez, amelynek ez lesz a szűrt értéke. Ezek a szűrők az úgynevezett rangszűrők. Az egyik legismertebb rangszűrő a medián szűrő, amely a sorba rendezett értékek sorban középső elemének értékét rendelik a pixel szűrt értékének. Az 13. ábrán egy idősorra alkalmaztuk a medián szűrőt.
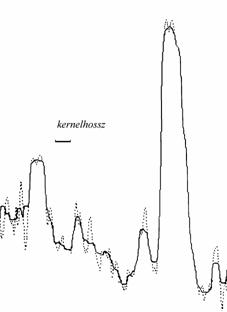
13. ábra
Egy egydimenziós függvény (szaggatott vonal)
és medián-szűrt változata (folytonos vonal)}
Jól megfigyelhető, hogy a fel- vagy lefutó éleken a szűrő nem változtatja meg az eredeti adatokat, hiszen azok az éleken már eleve nagyság szerint rendezettek. Nem éleken azonban erőteljesen simít. A simítás mértéke a kernel hosszától függ, annál jobban simít, minél hosszabb. E tulajdonsága miatt hatékony zajcsökkentő hatása is van.
Alul és felülvágó szűrők
Akkor használunk felülvágó szűrőt, amikor a frekvencia tartományban egy bizonyos
felső határfrekvenciánál (ff) nagyobb frekvenciákat 0-val szorzunk, és a nála kisebbeket 1-gyel. A 14. ábra mutatja az ideális felülvágás átviteli függvényét.
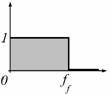
14. ábra
Az ideális felülvágás átviteli függvénye
Ami a frekvencia tartományban szorzás, az az időtartományban konvolúció, vagyis a jel időtartományban végrehajtott szűréséhez a négyszög függvény inverz Fourier-transzformáltját kell használnunk a konvolúcióhoz, amit két dimenziós esetre, mint amilyen a digitális kép, a 15. ábrán láthatunk.
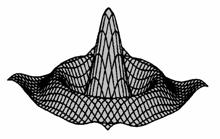
15. ábra
Az ideális felülvágás kernel függvénye az időtartományban két dimenzióban
Az alulvágás teljesen hasonló a felülvágáshoz, csak a két átviteli függvény összege 1 (azonos határfrekvenciára)
S(fa ) = 1 –S( ff ) |
Kép szín leválogató, cserélő, kivonó
Nagyon lényeges előkészítő funkció a kép megadott színű pixeleinek leválogatását lehetővé tevő eljárás. Ezzel levehetjük a képről ezeket a pixeleket, és elmenthetjük egy másik képben további feldolgozás céljára, mint például karakter felismerés. Ilyenkor a „üresen” maradt pixeleket a környezetük színével helyettesítjük.
Hasonlóan hasznos lehet, ha a leválogatott pixelek színét más színre állítjuk be.
Szegmentáló eljárások
A papírtérképek szkennelését minimum 24 bites mélységben végezzük, ezért a keletkezett állomány az eredeti papírnyomat színeinél sokkal többet tartalmaz. Alacsonyabb színmélységű szkennelés eredménye nem felel meg a céljainknak az operációs rendszer által alkalmazott színkódtáblák miatt. Ezért az eredeti kép színmélységét meg kell hagynunk, de csak annyi színállapotot engedhetünk meg, ahányat az eredeti nyomat készítői rá kívántak vinni a térképre. Ezért szegmentáló, csoportosító eljárásoknak is alá kell vetnünk a képeket.
A szegmentálás óriási témakör. Léteznek automatikus, statisztikai ismérvek alapján működő eljárások (pl. klaszter analízis), de a mi céljainkhoz ezeken kívül szükségünk van egy olyan eljárásra is, amely előre megadott számú szín-csoportba sorolja be a kép különböző pixeleit, de megtartja a 24 bites színmodell előnyeit. Egy térképész bármikor megmondja, hogy egy térképen hányféle szín található, és ennek megfelelően végezhető el a raszteres állomány színeinek átdolgozása.
A szegmentáló eljárások konkrét alkalmazását még számos elméleti kérdés viszgálata előzi meg, ezért ezeket jelen beszámolóban még nem ismertetjük.
Processzek és workflowk
A felsorolt eljárások csak kiragadott példák a fontosabb eljárások közül. Felvetődhet a kérdés, hogy ebben az eljárás dömpingben honnan fogja tudni a raszter-vektor konverziót végrehajtani kívánó felhasználó, hogy neki melyik eljárásra van szüksége, a lehetséges néhányszor tíz közül.
Ennek megkönnyítésére vezessünk be két fogalmat. Az egyik legyen az elemi process fogalma (16. ábra). Ezen elemi processzek legyenek azok a képmanipuláló eljárások, amelyekből válogathat a tapasztalt felhasználó, sőt maga is létrehozhat egy általa jónak tartott eljárást (plug-in).
A másik fogalom a workflow (16. ábra), amely több egymásba kapcsolódó, egymás után végrehajtandó elemi processz láncolatából áll. Egy cél elérése érdekében, (mint például, simított, zajszűrt kép) néhány elemi processzből álló workflow egy kényelmes eszközzé válhat. Így névvel hivatkozható, elmenthető, komplex eljárásokat kapunk. Tetszőleges workflowt állíthatunk elő az elemi processzekből attól függően, hogy mely folyamatok támogatják a leghatékonyabban az általunk elérni kívánt célt. Ez a tény azért lehet előnyös, mert egyrészt a felhasználó, a raszter-vektor konverziót végző szakember már kész workflowkat kaphat, másrészt maga is előállíthat az eddigiektől eltérő képességű workflowkat, amivel saját tudását is képes már az előfeldolgozó eljárások során beépíteni a konverziós eljárásba.
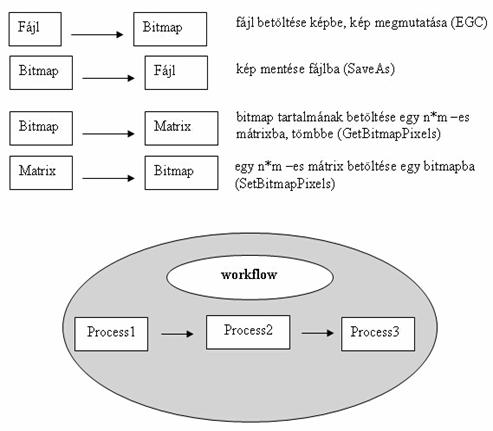
16. ábra
A workflow több elemi processzből épül fel, amelyek egymás után hajtódnak végre. Az egyik kimenete az utána következő bemenete lesz.
Az IRIS rendszer workflow editorának képét láthatjuk a 17. ábrán egy vektorizálásra váró raszteres állománnyal a háttérben.
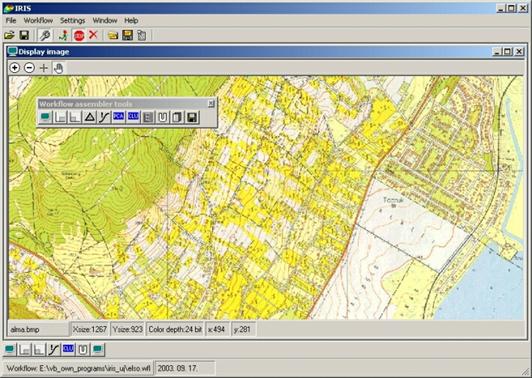
17. ábra
Az ábra közepétől balra láthatjuk az elemi processzek kollekcióját, amelyből összeállíthatjuk a workflowkat. Az ábra bal alsó sarkában egy már létező workflow elemi processzeinek grafikus szimbólumait láthatjuk. Ebből láthatjuk, hogy mit fog csinálni a workflow (megjeleníti az eredeti képet, alulvág, felülvág, medián szűr, szegmentál, megjeleníti az eredményt).
Nyers vektorizálás
Miután hatékony előfeldolgozó eljárásokkal előállítottunk ideális állományokat a vektorizáláshoz, megpróbálkozhatunk a konverzió első ütemével. Mint ahogy a bevezetőben említettük a vonalkövetés nem hatékony eszköz, ezért eleve a felültekre fogunk koncentrálni. Minden poligon lesz a nyers vektorizálás után. Az eljárásunkat nevezzük poligon-növesztésnek, amely következőképpen működik: induljunk ki a kép egy sarokpontjából. Vonjuk össze egy poligonná az összes azonos optikai állapotú (intenzitású, színű) pixelt, amelyek szomszédosak. Az azonos optikai állapotú, de diszjunkt pixelek új poligont eredményezzenek. Mindaddig növelünk egy poligont, amíg el nem fogynak az azonos optikai állapotú, érintkező pixelek. A folyamat eredményeképpen egy hézag és átfedésmentes topológiájú poligon struktúrát mutató vektoros állományt fogunk kapni, amin már minden vektorosan van rajta, ami a raszteres térképen rajta volt, de az adatstruktúra még nem célszerű, mivel sok objektum a természetétől teljesen idegen módon található meg a térképen (pl. a poligonok belsejéből hiányoznak a jelkulcs által kitakart elemek, sőt a jelkulcs elemek is poligonként látszanak, ami természetesen megszüntetendő anomália. Ezek utólagos orvoslása a következő feladat.
Itt ér véget az előfeldolgozás folyamata. Nem lehet további, „buta” eljárásokkal javítani a vektor állomány minőségén, főként a struktúráján. A további javítások már intelligenciát igényelnek, vagy emberit, vagy gépit.
Értelmezés
A másik fő feldolgozási fázis az értelmezés. Ebben már a térképolvasási képességek jutnak szerephez. A műveletek bemenete az előfeldolgozási fázis kimenete, vagyis a lehető legjobban előkészített kép alapján végzett nyers vektoros állomány.
A tudás reprezentációja
A tudás reprezentációja két tudásfajtát feltételez: egyrészt a jelkulcsban megbúvó tudást, másrészt a konvenciókat. A jelkulcsi elemek az alakfelismerés (pattern recognition) eredményei által válhatnak hozzáférhetővé, mivel a nyers állományon a jelkulcsban szereplő elemeket keressük. Amikor olyan mintázatot találunk, amely megfelel egy jelkulcsi elemnek, akkor a képen lévő poligont kitöröljük, és egy pontszerű jelkulcsi elemmel helyettesítjük.
A vonalelemek esetében a helyzet egyszerűbb, mert a vonal poligonként (vékony poligonként) szerepel a nyers vektoros állományban, de a térképen látható színével, így tehát eleve helyes lesz az optikai megjelenése (struktúrája még nem).
Ismert szöveg-felismerési probléma, hogy az OCR (Optical Character Recognition) szoftverek megvadulnak, ha a felismerendő szövegrészen áthúzások, vonalak mennek keresztül. Ezzel a jelenséggel térképek esetében is szembe kell néznünk, hiszen gyakran előfordul – főként topográfiai térképeken – hogy vonalak látszanak a megírások alatt. A probléma megelőzése céljából az előfeldolgozás során meg kell kísérelni a szöveget tartalmazó pixelek leválasztását a raszteres állományról (szín leválogató processz). Ha a szöveg színe eltér a többi térképi elemtől, akkor ez nehézség nélkül megtehető. Kevésbé szerencsés esetben, amikor nem szöveges objektumok is ugyanolyan színnel szerepelnek a térképen, is van esély a szétválasztásra. A szövegek cellákba rendezettek, a vonalak tetszőleges irányultságuak, vagyis a két objektumféleség eltérő habitusa alapján lehetséges a szétválasztás.
A konvenciók figyelembe vétele a következő példában látható módon lehetséges. Tegyük fel, hogy egy folyó középvonalán halad egy megye, egy nemzeti park határa és egy környezetvédelmi felügyelőség illetékességi területének a határa is. Ismert konvenció, hogy ilyen esetben nem rajzoljuk egymásra a három poligon határt, mert az túlzsúfolná a térképet, és ezzel rontaná az olvashatóságot, hanem megszakítjuk az egymásra következő poligonok határát mutató vonalat a közös szakaszon. A térképolvasó ember tudja, hogy a vonalak megszakadása ellenére ott egy poligon határa halad, pontosan az alatta lévő poligon határán. Ez a tudásfajta, mint konvenció, átadható, ráadásul a feldolgozás elején amúgy is definiálnunk kell, hogy az egyes objektumok a végső eredményben milyen geometriai típusúak (poligon, pont, vonal) legyenek.
Tervezés
A felsorolt néhány példából is látszik, hogy a konverziós folyamatot alapos tervezési munka kell, hogy megelőzze, ami persze nem meglepő a térinformatikai rendszerek építésében jártas szakemberek számára. Előre definiálnunk kell a vektorizálás során keletkező objektumcsoportokat. Ezek paramétereit be kell állítanunk (pont, vonal, poligon, megírás), a térképen való megjelenés attribútumait (jelkulcsi elem hivatkozás, vonaltípus, kitöltési mintázat, szín, stb.), a térkép fő típusát (pl. kataszteri, topográfiai, közmű), vagy bármely, ma még nem ismert, a felismerést javító paramétert.
Ami egyelőre nem várható az automatikus raszter-vektor konverziós eljárástól
Intelligensnek mondja a szakmai zsargon azokat az objektumokat, amelyek valamely olyan azonosítóval rendelkeznek, amely külső, például alfanumerikus adatok hozzákapcsolását is lehetővé teszik (például helyrajzi szám, településnév, stb.). Még ha sikerrel fel is tudjuk ismertetni a térképen látható neveket, feliratokat, annak automatikus eldöntése, hogy mely objektumra vonatkoznak, nem része a jelenlegi terveinknek, noha a térképészeti konvenciók ismeretanyagába elvben bevihetőnek látszanak ezirányú ismeretek is. Célkitűzéseink között egyelőre csak annyi szerepel, hogy a feliratok, mint karakterek leképeződjenek egy a beszúrási pontjukhoz rendelt pontszerű objektum attribútum adataként.
Előfeldolgozó workflowk és tudásbázisok tervezett előállítása
Egyelőre két térképféleség vektorizálásához állítunk elő (és még tervezünk előállítani) workflowkat és tudásbázist: a kataszteri térképekhez és az 1:10.000 topográfiai térképekhez. Az előzetes vizsgálatokból megállapítható, hogy a kataszteri térképek a látszat ellenére nem tűnnek sokkal egyszerűbb vizsgálati terepnek, mivel fekete-fehér mivoltuk miatt a színek nem segítik a feldolgozást. Egyéb szempontból viszont lényegesen egyszerűbb a kataszteri térképek vektorizálása. Itt nyilván nincs szerepe a színmanipuláló processzeknek, viszont annál nagyobb jelentőségű a zajszűrés.
Az IRIS csomag alkalmazása űrfelvételekre
A bemutatott kísérleti technológiát alapvetően papírtérképek vektorizálására használtuk eddig annak minden hibájával és gyermekbetegségével, és tervezzük használni a jövőben is. Belátható, hogy a műholdak által létrejött raszteres állományok esetleges vektorizálása nagyságrendekkel nehezebb feladat elé állítana bennünket, mivel részletgazdagságuk rendkívüli, és ráadásul semmiféle értelmezésen, generalizáláson nem estek át, mint a vektor térképek, amelyek a valóságnak az emberi intelligencia szűrőjén átment nagyfokú absztrakciói.
Egy dolgot világosan látnunk kell. Az, hogy mit látunk egy képen, nagyban függ az előképzettségünktől, az elvárásainktól, a háttértudásunktól, tapasztalatainktól, kultúránktól, előéletünktől.
Záró példám egy orvosi kép lesz, a mellkas egy computer tomográf által készített leképezése. Ez a kép számomra nem mond semmit, de a feleségem számára, aki több évtizedes gyakorlattal rendelkező orvos, egy nyitott könyv, amelyből feltárul a mellkas anatómiája, és esetleges anomáliái.
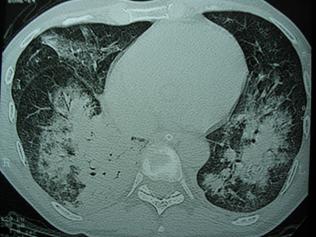
18. ábra
A mellkas computer tomográfos képe, amelynek értelmezése kizárólag több éves tanulás útján megszerzett háttértudás révén lehetséges
Felhasznált irodalom
1. M. Bellanger: "Digital Processing of Signals, Theory and Practice", John Wiley and Sons, 1986
2. Smith: "Digital Signal Processing", Elsevier Science, 2003
3. Plamondon "Pattern Recognition, Architectures, Algorithms & Applications", World Scientific Series in Computer Sciences - Vol.29
4. M. Nitzberg, D. Mumford, T. Shiota "Filtering, Segmentation and Depth", Lecture Notes in Computer Science 662
5. G. Kanizsa "Organization in Vision" New York: Preager, 1979, Ch.1-2.
6. Iványi A. "Informatikai algoritmusok", ELTE Eötvös Kiadó, 2004
7. J. F. Richards: "Remote sensing Digital image analysis", Springer-Verlag, 1986, Australia
8. Klinghammer – Papp-Váry: „Földünk tükre a térkép”, 1983, Gondolat, Budapest
9. J. Duncan: "The Elements of Complex Analysis", John Wiley & Sons, 1972
10. S. Russel - P. Norvig: "Mesterséges intelligencia, modern megközelítésben", Panem-Prentice Hall,2000
Fraktálgeometria a földtudományban
Bemutatunk egy lehetséges elméleti modellt, amely a porózus kőzeteket írja le a fraktálgeometria eszközeivel. Az alkalmazott elméleti megközelítés egy rekurziós módszerrel hoz létre szintetikus porózus kőzetet. A modellel igyekszünk megmagyarázni, hogy miért lehetséges nagy porozitás mellett csekély permeabilitás még abban az esetben is, ha a pórustér összefüggő, továbbá egységes leírásra tesz kisérletet úgy a porózus, mint a repedezett kőzetek esetében.
A Cantor-por
Georg Cantor, a neves német matematikus a XIX. században kitalált valamit, aminek úgy tűnt, hogy soha semmi köze nem lesz bármely gyakorlati probléma megoldásához. Elvont matematikai játéknak tetszett a műve, amit Cantor-halmaznak hívnak (mondják Cantor-pornak is). Számos ehhez hasonló csodabogár létezett és létezik ma is a matematikában. Nézzük meg, hogyan jön létre a Cantor-por.
Vegyünk egy vonalat. Távolítsuk el a középső harmadát. Ezután a megmaradt vonaldarabok középső harmadait is távolítsuk el és így tovább ad infinitum. A Cantor-halmaz tehát egy „porszerű” képződmény, amely a leírt rekurziós folyamat végrehajtása után megmarad. Igencsak különös tulajdonságai vannak. Csak egyet emelnék ki a sok közül: skálafüggetlen. A skálafüggetlenség nem egzakt megfogalmazás szerint azt jelenti, hogy bármelyik megmaradt harmadot nézem (bármilyen nagyításban), ugyanazt fogom látni, mint bármely más tartományban. A Cantor-halmazok jelentősége a jelátviteli hibák csökkentésekor mutatkozott meg. Nem véletlen, hogy Benoit Mandelbrot, a fraktálgeometria atyja, hívta fel rá a figyelmet.
Az 19. ábrán a Cantor-halmaz rekurziós lépéseinek eredményeit láthatjuk.

19. ábra
A Cantor-halmaz létrehozásának folyamata.
Az első öt lépés eredménye.
A Koch-görbe
Helge von Koch, svéd matematikus írta le elsőként a róla elnevezett görbét. A Koch-görbe tulajdonságai nem kevésbé különösek, mint a Cantor-poré. Nézzük meg, hogy hogyan állítható elő a Koch-görbe. Vegyünk egy szabályos háromszöget. Harmadoljuk el az oldalait, majd rajzoljunk az oldalak középső harmadára szabályos háromszögeket, ahogy a 20. ábrán látható. Az így előálló valamennyi háromszög oldalait harmadoljuk, majd rajzoljunk az oldalak középső harmadára szabályos háromszögeket, és így tovább a végtelenségig.

20. ábra
A Koch-görbe létrehozásának folyamata.
Az első három lépés eredménye.
A végeredmény rendkívül különös. Az egyik szembetűnő tulajdonság a skálafüggetlenség. Egy másik, talán még érdekesebb tulajdonság, hogy végtelen számú lépés után a görbe végtelen hosszú lesz, ugyanakkor sosem metszi önmagát, és egy véges térrészre korlátozódik a kiterjedése. Véges területen végtelen hossz.
A Sierpinsky-szőnyeg és a Menger-szivacs
Ez az alakzat úgy születik, hogy egy négyzet középső kilencedét kivágjuk (21. ábra), majd a maradék nyolc darab kilenced középső kilencedeit szintén kivágjuk, és így tovább ad infinitum.

21. ábra
A Sierpinsky-szőnyeg létrehozásának folyamata.
Az első három lépés eredménye.
Mindez három dimenzióban végrehajtva eredményezi a Menger-szivacsot (22. ábra), amely végtelen sok lépés után nulla térfogatú, de végtelen felületű lesz.

22. ábra
A Menger-szivacs a negyedik rekurziós lépés után
Amiről eddig szó volt, az fraktálok csodálatos világából néhány figyelemre méltó darab.
Fraktálok és kőzetfizika
A Menger-szivacs, mint elméleti modell, hasznosíthatónak látszik porózus kőzetek modellezésére. Ismert karotázs értelmezői tapasztalat, hogy vannak kőzetek, amelyek a karotázs mérések porozitásra érzékeny mérőberendezései által irreálisan nagy porozitásúnak látszanak. A végeredményben természetesen ezek az értékek már nem látszanak, mert okos programok a lehetetlen értékeket korrigálják, és lehetséges értékűvé „hazudják” őket. Nem lehetetlen, hogy ezen értékek jelenléte nem mérési hibára vezethető vissza, hanem a fraktálgeometria érvényesülését jelzi.
További érdekes tapasztalat, hogy az egyes mérőberendezések által nagynak mutatott porozitású kőzetek, csekély effektív pórusterűek (ahol folyadékok tartózkodhatnának, mint például víz, olaj), sőt sokszor e kőzetek csekély permeabilitással is rendelkezik.
A Menger-szivacs modell segítségével számítsuk ki, hogy mekkora pórustér fog keletkezni az egyes rekurziós lépések után. Vegyünk egy a élhosszúságú kockát, ahogy az 23. ábrán látható. Hajtsuk végre az első iterációs lépést, és számítsuk ki a porozitást.
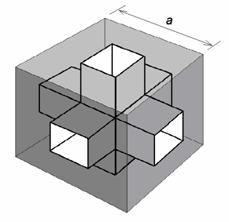
23. ábra
Az első rekurziós lépés során keletkezett pórustér az a élhosszúságú kockában.
A fehéren látható részek ábrázolják a pórusteret.
A kocka tömör anyagának térfogata az első rekurziós lépés előtt
V = a3.
Az első iterációs lépéssel keletkező pórustér térfogata:
Vp = 7 (a/3)3
A maradék tömör anyag térfogata:
Vb = a3 – 7 (a/3)3 = 20 (a/3)3
A porozitás: F = Vp / V = 7 (a/3)3 /( 27 (a/3)3) = 7 /27 = 0,26
Az első rekurziós lépés tehát hozzávetőlegesen 26 %-os porozitást eredményez.
A második rekurziós lépés kiszámításához használjuk a Menger-szivacs skálafüggetlen tulajdonságát. 7 darab, a/3 élhosszúságú üres kockánk van, tehát a további felosztást a maradék 20 kockán végezhetjük. Egy ilyen kocka térfogata (a/3)3. Minden egyes kocka felosztása révén újabb 7/27 résznyi pórustér keletkezik. Ezt hozzáadva az első rekurziós lépésben kapott pórustérhez azt kapjuk a porozitásra, hogy
F = 7/27 + 20*(7/27)/27 = 0,45
A második rekurziós lépés tehát hozzávetőlegesen 45 %-os porozitást eredményezett.
Gondoljuk tovább a folyamatot. A rekurziós algoritmus előrehaladásával a pórustérfogat a következőképpen alakul:
Vp = S Vp(i)
ahol Vp az i-edik lépés utáni teljes pórustérfogat, Vp(i) az i-edik lépéssel keletkező pórustérfogat hányad. Ha i ® µ , akkor Vp ® 1.
A tapasztalat azt mutatja, hogy porózus kőzetek esetében is gyakran lehet nagyon alacsony a permeabilitás. A nagy pórustérfogat, gondolhatnánk, nagy permeabilitással jár együtt, ha nem zárvány porozitás teszi ki a pórustér java részét, vagy nem tölti ki a pórusteret valamilyen másodlagos folyamat által behordott finomszemcsés kőzetanyag. Az alacsony permeabilitás oka a kőzetanyag nagy felületében, és a felületi feszültségben keresendő. Jelölje s a felületi feszültséget,
s = Fh / Ah ,
ahol Fh a határoló felületen ható erő, Ah a határoló felület nagysága. Ebből az egyszerű összefüggésből látható, hogy annál nehezebb lesz egy adott viszkozitású folyadéknak mozogni a pórustérben, minél nagyobb felülettel rendelkezik a pórustér. A fraktálgeometriai kőzetmodellből látható, hogy igen bonyolult szerkezetű, és nagy felületű porózus kőzetben valóban előfordulhat, hogy a benne lévő folyadék nem lesz képes mozgásra.
Ne felejtsük el, hogy hiába skálafüggetlen a Menger-szivacs, ha a felületi feszültség nem az. Nagyon is behatárolt az a mérettartomány, ahol a kapilláris jelenség dominánssá válik. Ebből levonhatjuk azt a következtetést, hogy a Menger-szivacs jó modellje lehet a porózus kőzeteknek, mert bizonyos mérettartományokban képes megmagyarázni az alacsony permeabilitást nagy porozitás mellett, míg más mérettartományokban, ahol a felületi feszültség hatása már nem számottevő, a nagy porozitású, permeábilis kőzetek viselkedését is jól leírja.
Joggal vetődhet fel a kérdés, hogy miért jobb ez a megközelítés, mint apró gömböcskékkel kitölteni egy kockát, és annak kiszámítani a porozitását. Nos, egyáltalán nem biztos, hogy a porózus kőzetek fizikáját jobban írja le a fraktálokkal felvázolt modell. Az azonban biztos, hogy olyan kőzetek porozitását, amelyek tektonikus folyamatok által keltett repedésekből állnak, a kőzetgömbökkel manipuláló modell nem képes megmagyarázni. Érdekes viszont, hogy a szeizmológusok által végzett vizsgálatok azt mutatják, hogy a földrengések által keltett repedésrendszerek eloszlása fraktálgeometriai jellegzetességeket mutat. Ez alapján lehet némi reményünk, hogy a repedezett kőzetek porozitás—permeabilitás összefüggéseinek feltárásában szerepet kaphat a fraktálgeometria.
Felhasznált irodalom
- Mandelbrot: „The Fractal Geometry of Nature”, Freeman, 1982
- Szépfalusy-Tél: A káosz. „Véletlenszerű jelenségek nem lineáris rendszerekben”, Akadémiai kiadó, 1982
- Barabási, Albert, Jeong: „Mean-field theory for scale-free random networks”, Preprint submitted to Elsevier Preprint, 5 July 1999.
- Albert, Barabási: „Statistical mechanics of complex networks”, Reviews of modern physics, VOLUME 74, January 2002