5.2. Egyenesekkel határolt síkidomok területe

Egyenesekkel határolt síkidomok esetén, legyenek azok bármilyen bonyolultak, célravezetőbb a számítás, mint bármilyen konkrét területmérési eljárás. Ilyen alakzatok területmérése a kataszteri, földmérési térképeken igen gyakori feladat, lévén a mérendő birtokterületek, művelési parcellák szinte mindig egyenesekkel határoltak. Az ilyen térképeken a közvetlen terepi mérésekből kapott oldalhosszak is fel vannak tüntetve és így a terület számításához tulajdonképpen már kartometriai hosszmérésre sincs mindig szükség.

Az ilyen, jórészt számításokon alapuló módszerek pontosságát két tényező befolyásolja:

  1. milyen pontosak az adataink, milyen pontos volt a geodéziai felmérés, illetve milyen pontosan tudunk távolságokat lemérni a térképen;
  2. a számítási eljárások matematikai pontossága, a kerekítések hatása.
Az egyenesekkel határolt idomok egy speciális esete a foktrapéz. Ez olyan négyszög, melynek szemközti oldalai meridiánok, illetve parallelkörök. S bár ezek a valóságban gömbi főkörök, a térképen - a vetülettől függően - lehetnek egyenesek, de általában görbe vonalak. Természetesen egy foktrapéz területének meghatározása igazából kis méretarányú térképeken problematikus, hiszen nagy méretarányban a földrajzi hálózati vonalak egyenesekként képződnek le a vetítés során (valójában nem azok, csak a nagy méretarány miatt látszanak annak).

A foktrapéz területe a következő közelítő képlet segítségével 10-5 pontossággal számítható ki [2]:

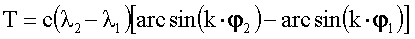
ahol c=75456.835 km2 és k=0.163133 a Kraszovszkij-ellipszoid esetében.


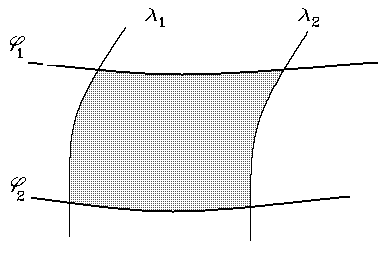
5.1. ábra Foktrapéz.
4bal.gif - 1.0 K 4fel.gif - 1.0 K 4jobb.gif - 1.0 K
© Zentai László
Vissza a Térképtudományi és Geoinformatikai Tanszék kezdőlapjára!