9.2.3. A beszivárgási adatokra készült térképek
A térképeken jól látszik, hogy a program a két legtávolabbi pontra (Keszthely–Nézsa) húzza rá a legkisebb téglalapot, és az így kialakított területre számol. Ezeknél az adatoknál, a Surfer nyújtotta lehetőségeket kihasználva, kétfajta módszerrel is szerkesztettünk térképeket:
krigeléssel és a távolság négyzetével fordítottan arányos súlyozással. Ennek az oka az, hogy ha az empirikus félvariogram röghatás típusú, akkor a területre számított beszivárgási (vagy a térkép tárgyaként szolgáló bármely) adatok olyan távol vannak egymástól, hogy nincsenek egymásra hatással. Így nem illeszthető elméleti félvariogram az empirikus félvariogramra, következésképpen nem szerkeszthető lineáris becslési eljárással térkép. (9. ábra)
Ennek ellenére – bár helytelen – a meghatározott hatástávolságokkal elkészítettük a krigelt térképeket is.
Krigeléssel készült térképeknél a különböző beszivárgás-számítási módszerekhez a következő hatástávolságokat határoztuk meg:
Böcker: 25 km
Kessler1: 20 km
Kessler2: 15 km
Maucha: 18 km
Morton: 30 km

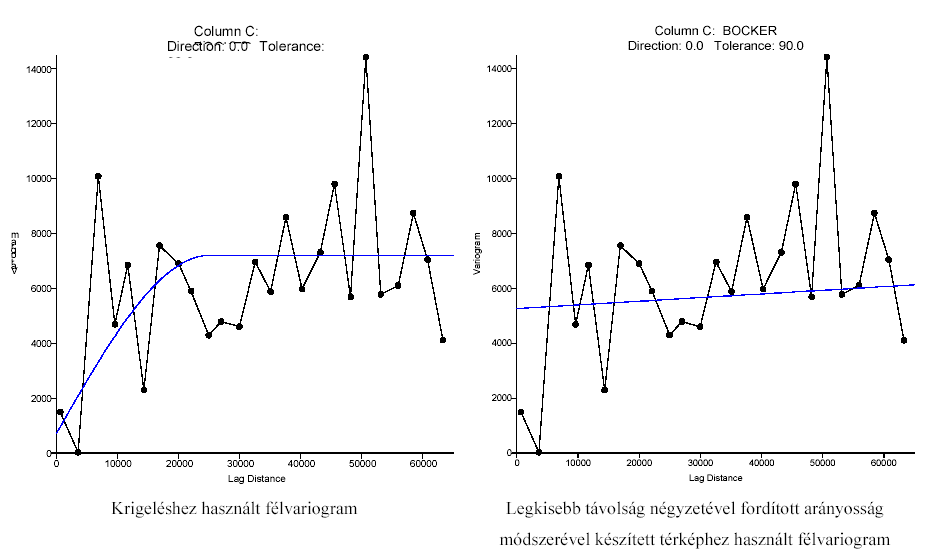
9-2-3-a.gif - 18319 Bytes
9. ábra

Variogram A hatástávolságok nagysága meghatározza a térkép arculatát. Látható, hogy a kis hatástávolság miatt a Kessler- és a Maucha-féle számítási módszerek adataival készült térképek változatos képet mutatnak. A Morton-féle módszerrel számított adatokból, ahol nagy hatástávolságot határoztunk meg, sokkal kiegyenlítettebb „morfológiát” mutató felületet kaptunk. Itt és a későbbiekben is többször látható lesz, hogy a nagy hatástávolság miatt olyan területekre is történt becslés, ahol nem volt konkrét mérési adat.
A távolsággal fordítottan arányos súlyozással kapott térképek szakmailag a mért adatok területére teljesen elfogadhatónak tűnnek. Ezzel szemben az adathiányos területekre extrém értékeket becsült a Surfer (4. melléklet, 91-95. oldal). Ha a program meg tudná tenni, hogy korrekt módon elvégezze a terület lehatárolását, akkor egy tetszetős és szakmailag is korrekt térképet kapnánk.

Vissza a Térképtudományi és Geoinformatikai Tanszék kezdőoldalára!