A 2![]() függvényt a paraméter variogramjának, a
függvényt a paraméter variogramjának, a ![]() függvényt pedig a
félvariogramjának nevezzük. A félvariogramot a telep térfogatára vonatkozóan a következő
összefüggéssel határozhatjuk meg:
függvényt pedig a
félvariogramjának nevezzük. A félvariogramot a telep térfogatára vonatkozóan a következő
összefüggéssel határozhatjuk meg:
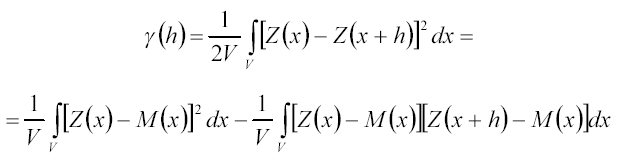
22
Az előbbi összefüggés szigorúan véve csak a paraméter normális eloszlással való közelíthetősége esetén érvényes, de alkalmazható olyan eloszlástípusok esetében is, amelyek
megfelelő transzformációval normálissá alakíthatók. A normálisra közvetlenül nem visszavezethető eloszlástípusokkal közelíthető paraméterek esetében a félvariogramot és az
autokovariancia függvényt csak közelítőleg tudjuk meghatározni. Általánosságban ilyenkor a
normális eloszlásnál megismert összefüggéseket szokták alkalmazni. Számos geostatisztikus
nem tulajdonít jelentőséget a paraméterek eloszlástípusának. Az eloszlás figyelmen kívül
hagyása azonban jelentős tévedések forrása lehet. Ezért célszerű a mérési eredmények
normalizálása, majd a normalizált adatok használata a félvariogram és az autokovariancia
függvényhez.
Meg kell említeni a robusztus variogrambecslést, mert a kovarianciastruktúra akkor jó,
ha Gauss-folyamatot vizsgálunk. A valóságban azonban gyakran nem pontos a Gaussilleszkedés.
Ezért olyan becslés kell, ami kicsit „eltérő” adatokra is jól becsüli a variogramot.
A variogrambecslésnél már egy kiugró adat is nagyon elronthatja a becslést, mert a négyzetét
vesszük, és úgy átlagoljuk. Ezért vegyük először a különbségek négyzetgyökét, átlagoljuk, és
emeljük a negyedik hatványra. Nem véletlenül választjuk a négyzetgyökvonást és a negyedik
hatványra történő emelést, hiszen az eloszlás így lesz a leginkább Gauss-eloszláshoz hasonló.
Az ilyen becslést hívják robusztus becslésnek. A robusztus becslés képletében szereplő
konstansokat a torzítás kompenzálására találták ki. Ennek a módszernek csak akkor van
előnye, ha az adataink nem illeszkednek elég jól a Gauss-eloszlásra, ha illeszkednek, a
robusztus becslés nem lesz jobb. Célszerű a variogramot mindkét eljárással becsülni.


